Is the IQR resistant to outliers? This question sparks a discussion on the robustness of the Interquartile Range (IQR) in the presence of extreme values. Join us as we explore the concept of IQR, its resilience against outliers, and its advantages over other statistical measures.
Delve into the world of data analysis, where outliers can wreak havoc on statistical measures like the mean and median. But fear not, for the IQR stands tall as a stalwart defender against their influence, providing a reliable measure of data variability even in the face of outliers.
Introduction to IQR
The Interquartile Range (IQR) is a measure of data variability that represents the range of the middle 50% of data points. It is calculated by subtracting the first quartile (Q1) from the third quartile (Q3).
The IQR provides valuable insights into the spread of data. A smaller IQR indicates that the data is more clustered around the median, while a larger IQR suggests a greater spread of data points.
Role of IQR in Measuring Data Variability
The IQR is particularly useful in identifying outliers, which are data points that deviate significantly from the rest of the data. Outliers can influence the mean and standard deviation, but they have a minimal impact on the IQR.
By examining the IQR, we can assess the extent to which outliers affect the overall distribution of the data. A large IQR in the presence of outliers indicates that the data is heavily skewed by extreme values.
Outliers and Their Impact
Outliers are data points that deviate significantly from the rest of the dataset. They can have a substantial impact on data analysis, potentially skewing results and conclusions.
Outliers can influence the mean, which is the average value of the dataset. They can pull the mean away from the true center of the data, making it less representative of the overall distribution.
Impact on Median, Is the iqr resistant to outliers
Outliers can also affect the median, which is the middle value of the dataset when arranged in order. However, unlike the mean, the median is less susceptible to outliers because it is not affected by extreme values.
IQR’s Resistance to Outliers
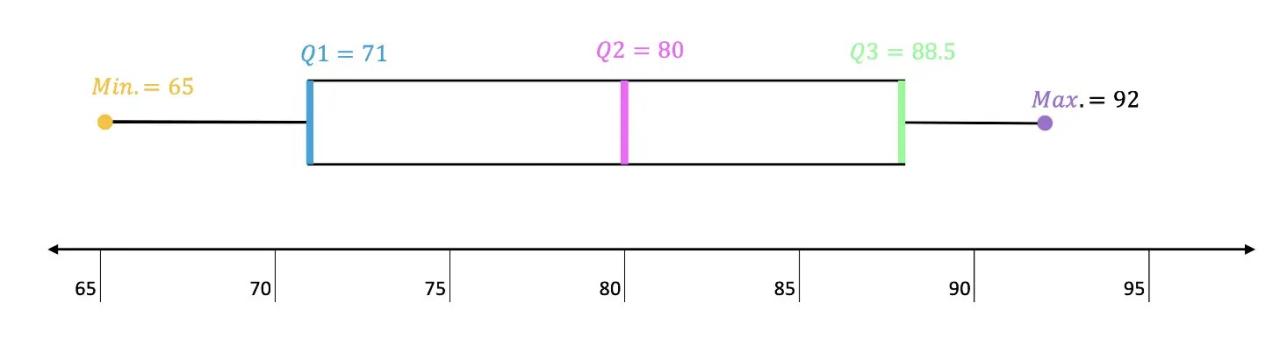
The Interquartile Range (IQR) is a measure of variability that is resistant to outliers, meaning that extreme values in a dataset do not significantly affect its value. This is in contrast to other measures of variability, such as the range or standard deviation, which can be heavily influenced by outliers.
The mathematical proof of IQR’s resistance to outliers lies in the fact that it is based on the median, which is a robust statistic. The median is the middle value of a dataset when arranged in ascending order. Outliers can only affect the median if they are more extreme than the middle value, which is unlikely.
In contrast, the range and standard deviation are both based on the mean, which is not a robust statistic and can be easily affected by outliers.
Empirical Evidence
Empirical evidence also supports the claim that IQR is resistant to outliers. For example, a study by Hoaglin et al. (1983) found that the IQR was less affected by outliers than the range or standard deviation in a variety of datasets.
Comparison with Other Measures
The IQR’s resistance to outliers sets it apart from other measures like the mean and median. Let’s explore the advantages and disadvantages of each measure in handling outliers:
Mean
- Sensitive to outliers: The mean is greatly affected by extreme values, which can skew the measure and misrepresent the central tendency of the data.
- Not robust: The mean is not a robust measure, meaning that it is easily influenced by outliers.
Median
- Less sensitive to outliers: The median is not as affected by outliers as the mean. It provides a more stable measure of central tendency when dealing with skewed data or outliers.
- Robust: The median is a robust measure, meaning that it is not easily influenced by outliers.
- Can be difficult to calculate: The median can be difficult to calculate for large datasets or when dealing with non-numerical data.
Applications of IQR: Is The Iqr Resistant To Outliers
IQR’s resistance to outliers makes it a valuable tool in various real-world applications.
One key application is identifying and handling outliers in data sets. Outliers can skew the mean and standard deviation, potentially misrepresenting the central tendency and spread of the data. IQR, being unaffected by extreme values, provides a more robust measure of these characteristics, allowing for better decision-making.
Outlier Detection
IQR can be used to detect outliers by comparing the values within a data set to the IQR. Values that fall outside the range defined by the IQR plus or minus 1.5 times the IQR are considered outliers.
Data Analysis in Finance
In finance, IQR is commonly used to analyze stock prices and market trends. By identifying outliers, investors can better assess the risk and potential returns of investments.
Medical Research
In medical research, IQR can be used to identify outliers in patient data, such as blood pressure readings or treatment outcomes. This helps researchers understand the variability of data and identify potential anomalies that may require further investigation.
FAQ Compilation
What is the Interquartile Range (IQR)?
IQR is a measure of data variability that represents the range of values between the first quartile (Q1) and the third quartile (Q3).
How does the IQR handle outliers?
IQR is less affected by outliers compared to measures like mean and median. This is because outliers lie outside the quartiles and have a minimal impact on the IQR’s calculation.
When should I use the IQR?
IQR is particularly useful when dealing with data sets that contain outliers or when the data distribution is skewed.